Bounding eigenvalues of a matrix using the Gershgorin disk theorem
A method to approximate the spectrum of a matrix.
The beauty of the Gershgorin disk theorem
In this post I’ll talk about one of the most beatiful theorems I’ve encountered while studying linear algebra. I bumped into it while taking the ACM104 Applied Linear Algebra course at Caltech, taught by Prof. Kostia Zuev. As the name of the course suggests, this theorem has a lot of applications, one of which we will explore in the end, so if you’re here for the applications, read on! The math can seem a bit hairy if you skim over quickly, but I assure you that it is actually surprisingly simple.
Disclaimer: The “applications” in the bottom of this post are to understand better certain groups of matrices. For a “real application” of the theorem, in my next post I will use it for an actual algorithm you can use to visualize your data. If you’re more interested in the latter, hang tight.
I find this theorem aesthetically pleasing because it has a visual representation. Moreover, I think that the wit with which it came about (by the short-lived mathematician Semyon Gershgorin) is to be praised for. It is a clear example of how mathematics are just right there, waiting to be discovered.
We follow the proof of the book Applied Linear Algebra by Olver and Shakiban.
Preliminaries
Before stating the theorem, we’ll need some definitions. Recall that the magnitude of a complex number \(z = a + ib\) is defined by
\[|z| = \sqrt{a^2 + b^2}\]If we define the conjugate, we can compute the magnitude as follows:
\[\bar{z} = a - ib, |z|^2 = z \bar{z}\]Definition. Gershgorin disk. Let \(A \in \mathbb{M}_{n \times n}\) a matrix over \(\mathbb{F}\) (either \(\mathbb{R}\) or \(\mathbb{C}\)).
For each \(1 \le i \le n\), define the \(i\)-th Gershgorin disk as :
\[\begin{align} D_i = \{ |A_{ii} - z_i | \leq r_i : z \in \mathbb{C} \}\\ r_i = \sum_{j = 1, j \neq i} | A_{ij} | \end{align}\]I know this definition can be not quite intuitive so let me break it down. In words, the i-th Gershgorin disk of a square matrix A is just a closed ball centered at \(A_{ii}\) with radius equal to the sum of the absolute value of the off-diagonal elements of the i-th row. By construction this ball will live in the complex plane. To keep things simple and start building a mental picture of the theorem, you can think of a single Gershgorin disk as simply a disk or closed ball (a filled circle) in the Cartesian plane.
Definition. Gershgorin domain. The union of the \(n\) Gershgorin disks is the Gershgorin domain.
\[\mathfrak{D}_A = \{ \cup_{i = 1}^n D_i \} \subseteq \mathbb{C}\]We visualize the Gershgorin domain of a matrix in the image below:
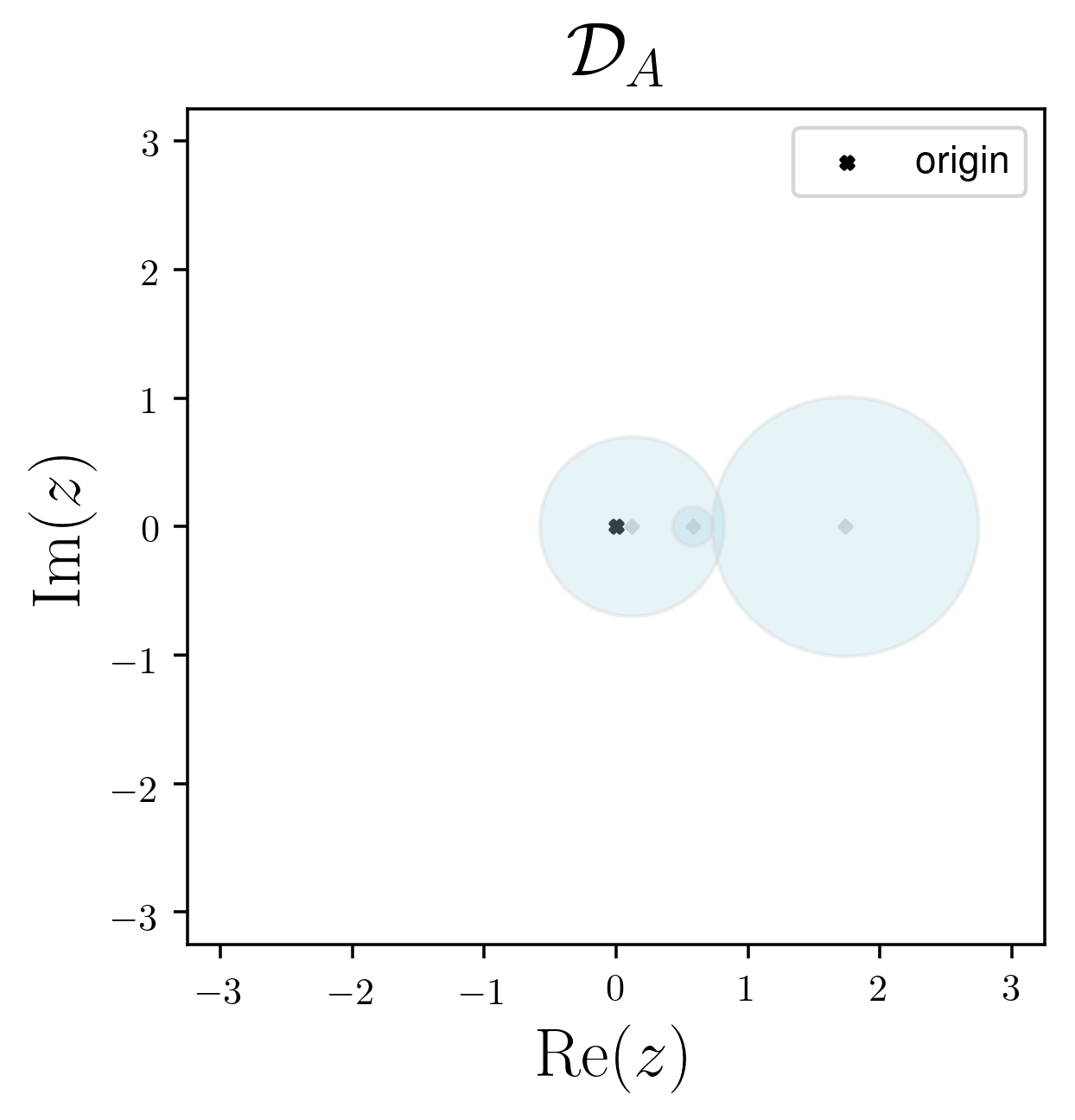
Definition. Spectrum of a matrix. We call the spectrum of a matrix A to the set of eigenvalues associated with A. We denote it as \(\mathrm{spec} A\).
The statement
Theorem. The spectrum of a matrix A lies within the Gershgorin domain.
\[\mathrm{spec A} \subseteq \mathfrak{D}_A \subseteq \mathbb{C}\]Proof: The constructive proof is surprisingly straightforward.
Let \(\lambda\) be an eigenvalue of A, \(\vec{v}\) be its associated eigenvector. Let \(\vec{u} = \frac{v}{ || v ||_{\infty} }\) be the corresponding unit eigenvector with respect to (w.r.t.) the \(\infty\) norm, i.e.
\[|| u ||_\infty = \mathrm{max} \{ |u_1|, ..., |u_n| \} = 1\]Let \(u_i\) be an entry of \(\vec{u}\) that achieves the maximum \(\mid u_i \mid = 1\). Writing out the i-th component of eigenvalue equation we obtain:
\[\sum_{j = 1}^ n \mathbf{A}_{ij} u_j = \lambda u_i\]which we can rewrite as:
\[\sum_{j \neq i } \mathbf{A}_{ij} u_j = \lambda u_i - \mathbf{A}_{ii} u_i = (\lambda - \mathbf{A}_{ii} ) u_i\]Note: in the last step we just subtracted \(\mathbf{A}_{ii}u_i\) from both sides.
Thus, since all \(\mid u_j \mid \le 1\) while \(\mid u_i \mid = 1\) we have that
\[\begin{align} |\mathbf{A}_ii - \lambda| &= |\lambda - \mathbf{A}_{ii}| \\ &= |\lambda - \mathbf{A}_{ii}| |u_i|\\ &= | (\lambda - \mathbf{A}_{ii}) u_i | \\ &= | \sum_{j \neq i} \mathbf{A}_{ij} u_j | \\ &\le \sum_{j \neq i } |\mathbf{A}_{ij}| |u_j| \\ &\le \sum_{j \neq i} |\mathbf{A}_{ij}|\\ &= r_i. \end{align}\]We have equality in the third step as can be checked for all cases ( ++, +-, -+, – ). The fourth step is just substituting the equation above. The fifth step holds by the triangle inequality \(||x+y|| \le ||x|| + ||y||\). The sixth line holds as \(|u_j| \le 1 \forall j \neq i\) by construction of \(\vec{u}\).
This implies the following:
\[|\lambda - \mathbf{A}_{ii}| \le r_i \implies \lambda \in D_i\]An immediate corollary is related to the invertibility of square matrices.
Definition. A square matrix is called diagonally dominant if
\[|a_{ii}| > \sum_{j \neq i} |a_{ij}| \forall i = 1, ..., n.\]Corollary. A strictly diagonally dominant matrix is nonsingular.
Proof: A matrix is singular iff it admits zero as an eigenvalue (an eigenspace shrinks to zero \(\implies \mathrm{dim }\, \mathrm{ker} \ge 1\). ). Thus, if its Gershgorin domain doesn’t contain zero, it cannot be an eigenvalue, hence A is necessarily invertible / non-singular.
Theorem. A symmetric matrix is positive definite if all of its eigenvalues are positive.
Corollary. A symmetric matrix is positive definite if its Gershgorin domain lies in the positive side of the \(\mathbb{C}\) plane. In other words, a matrix is p.d. if \(a_{ii} > \sum_{j\neq i} a_i \forall i = 1, ..., n.\).
Examples
Here are some visualizations in a jupyter colab notebook if you want to get a feel of the theorem.